Blog

Java solution for checking if a string is a palindrome

Introduction

A palindrome is a word that reads the same forward and backward. In this article, we will write logic to check if the input string is palindrome or not.

Checking for Palindrome

Palindromes are words that read the same backward and forward. For example, consider the word RACECAR, if we read it backward it will be the same as reading forward.

In order to write a logic to check the palindrome, we can use 2 pointers and travel them inwards. while doing that we can equate the characters. we can do this until two pointers either are on the same index or cross each other.

While moving indexes inwards if we see the case where characters are not matching then we can immediately return false otherwise we return true once we finish the iteration.

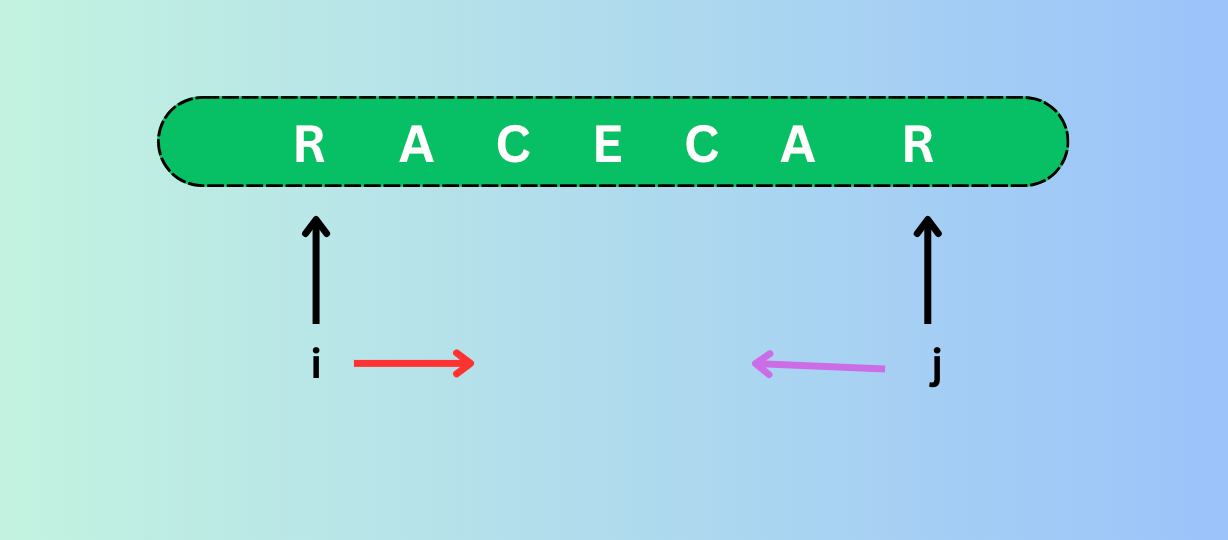
Pseudocode

define two pointers, left and right. 
   - left = start and right =end of string
     int i=0;
     int j=s.length()-1;

move the window
   - if char at left and char at right are equal keep shrinking the window
   - if char at left and char at right are not equal return immediately
     
     while(i<j){
        if(s.charAt(i)!=s.charAt(j)){
            return false;
        }
        i++;
        j--;
     }
     return true;

Code

Iterative

• As explained above, we will have two pointers i and j that will keep moving inwards until it’s either find a situation where two chars at I and j are not equal or they cross or arrive at the same position.

public boolean validate(String s){
    int i=0;
    int j=s.length()-1;
    while(i<j){
        if(s.charAt(i)!=s.charAt(j)){
            return false;
        }
        i++;
        j--;
    }
    return true;
}

Recursive

• Recursive solution is not that different from than iterative one. the only difference is that we call for each window in recursion instead of iterating over for loop. Overall logic remains similar.

public boolean validateRec(String s, int left, int right){
    if(left>=right){
        return true;
    }

    if(s.charAt(left)!=s.charAt(right)){
        return false;
    }

    return validateRec(s, left+1, right-1);
}

Testing

• Let’s test our logic using the unit test.

@Test
public void givenPalindromesInputString_whenIsValid_thenReturnsTrue(){
    List<String> palindromes = List.of("ABA", "AA", "CCACC");
    palindromes.forEach(p -> {
        PalindromeCheck pc = new PalindromeCheck();
        boolean actual = pc.validate(p);
        assertEquals(true, actual);
    });

    palindromes.forEach(p -> {
        PalindromeCheck pc = new PalindromeCheck();
        boolean actual = pc.validateRec(p,0,p.length()-1);
        assertEquals(true, actual);
    });
}

• Also, let’s test recursive solutions as well.

@Test
public void givenNonPalindromesInputString_whenIsValid_thenReturnsFalse(){
    List<String> nonPalindromes = List.of("ABAA", "AAP", "CACC");
    nonPalindromes.forEach(p -> {
        PalindromeCheck pc = new PalindromeCheck();
        boolean actual = pc.validate(p);
        assertEquals(false, actual);
    });

    nonPalindromes.forEach( p -> {
        PalindromeCheck pc = new PalindromeCheck();
        boolean actual = pc.validateRec(p,0,p.length()-1);
        assertEquals(false, actual);
    });
}

Complexity

Time complexity:
Since we are traversing the loop, time complexity would be O(N).

Space complexity:
Space complexity remains constant since we are not using any data structure to store data.

Conclusion

In this article, we learned about palindromic string. We discussed and coded two solutions one with an iterative solution and the other with recursion. Time complexity is O(N) while space complexity is O(1).

Code used in this example is available at github.

Before You Leave

• Crack DSA interview with Mastering Leetcode In Java — Top 100 Most Asked Problems
• Crack SQL Interview With Grokking the SQL Interview [Free Sample Copy]
• Subscribe to Java Newsletter to keep up with all the updates in Java/Spring world.