Introduction

In this article, we will solve the leetcode 131 problems which help us to learn about backtracking/recursion on String.

Problem Statement

We are given as String s. We need to partition s such that every substring of the partition is a palindrome.
We need to return all the possible palindrome partitioning of s.

Example #1

Input: s = "aab"
Output: [["a","a","b"],["aa","b"]]

Example #2

Input: s = "a"
Output: [["a"]]

Thinking About Solution

The first thing that comes to mind is that if we can take a substring of String and s and check if it is a palindrome and if it does then we can add it to our result list.
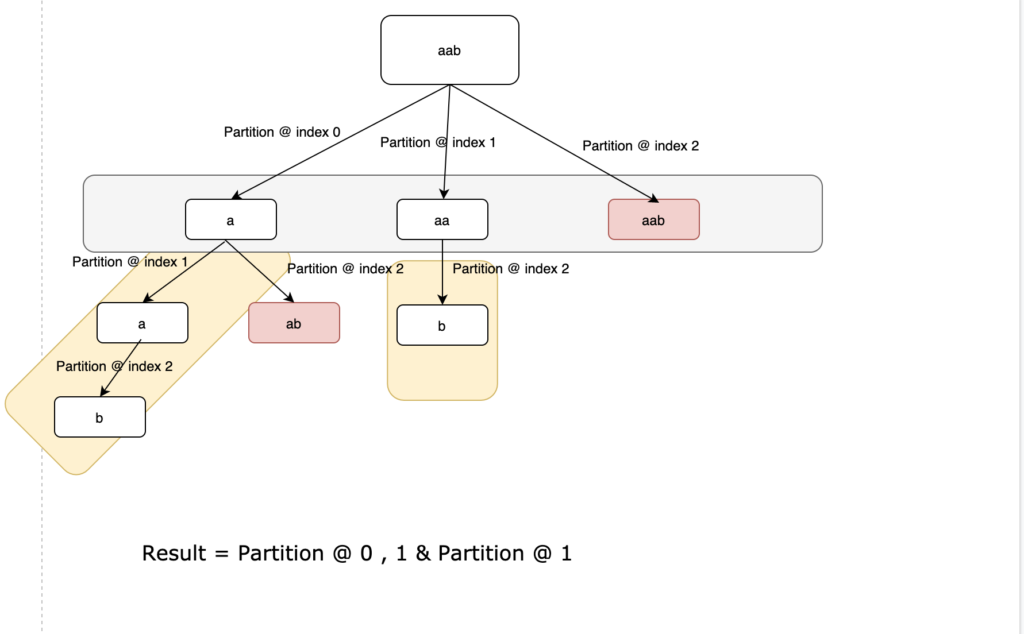
We can partition given String it in various ways, for example, if given string s = “aab”, then we can either partition it as p1 = [ “a”,”a”,”b” ] or p2=[ “a”,”ab”] or p3 =[ “aab” ] . As for p1, we can say each substring is palindrome since a single character string is always palindrome. But for p2, although “a” is a palindrome, “ab” is not a palindrome hence we cannot take that partition as a solution. The same goes for p3.

So our solution should iterate string s for various combinations and we should check each substring for palindrome.

What would be the criteria to output our result, since some substring in our partition can be palindrome and some might not as we saw in p2. The best way to confirm if all the substring is a palindrome is that check the index whether it reached the end of String s , because if all the substrings are palindromic then the index would reach the end of string otherwise it will not move forward. And that would make our base case.

For loop would be required to create a partition at the index at the various positions and then we need to recursively call to check for the selected index can we do further partition so that we make all the substring palindromic.
In the Below diagram, The gray box is the role of for loop and the yellow box is where recursion will play its role.

Solution

class Solution {
    // Result List to collect the palindrome of partition
    List<List<String>> result = new ArrayList<>();

    public List<List<String>> partition(String s) {
       // List of all current palindromic partition
        List<String> currPartition = new ArrayList<>();
        partition(s,0,currPartition,s.length());
        return result;
    }
    
    private void partition(String s, int i, List<String> currPartition, int len){
        // base case to check if the index i reched to the end of string s
        // if it does then we can simply copy the result and return the call
        if(i>=len){
           // System.out.println(currPartition);
            result.add(new ArrayList<>(currPartition));
            return;
        }
        
        // lets iterate over string s from j=initial index i upto end of string s
        for(int j=i;j<s.length();j++){
            String target = s.substring(i,j+1); // take the substring from i upto j
            System.out.println("target : "+target);
            if(isPal(target)){ // check if target substr is palindrome
               // if it is then add to current partition
                currPartition.add(target); 
                // next recursively check other substrings by increasing initials . for example "a" is palindrome, then next target would be next "a" and then next "b".
                partition(s,j+1,currPartition,len);
                /** since we already checked for current substring , then lets remove it from our currentPartition and check for another combination
like initially we check for combination "a", next we will check for combination "aa" and then finally for "aab" **/
                currPartition.remove(currPartition.size()-1);
            }
    }
}
    // boiler plate code for checking if a string is palindromic or not
    private boolean isPal(String s){
        int i=0;
        int j=s.length()-1;
        char[] schar = s.toCharArray();
        while(i<j){
            if(schar[i]!=schar[j]){
                return false;
            }
            i++;
            j--;
        }
        return true;
    }
}

Result

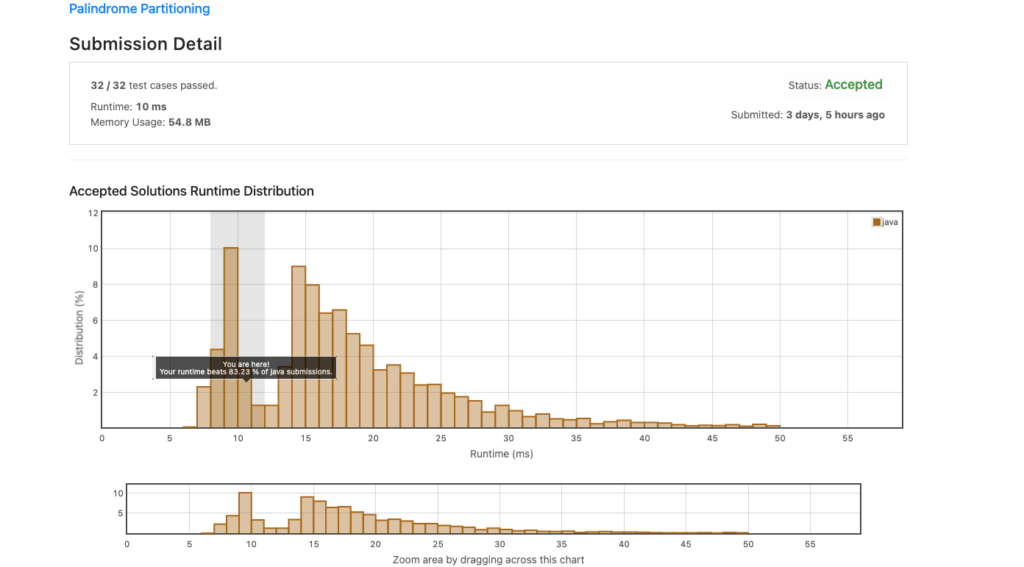
Our submission does get accepted with a runtime of 10 ms and beats 83% of solutions.

Space Complexity: O(N) for our recursion call to store N substring.
Time Complexity: O(N*2^N) where N is the length of the substring. For loop = N, recursion = 2^N is a worst-case scenario where we have to break a partition into two substrings at every level.

Conclusion

In this article, we solved leetcode problem # 131, which helps us to understand how backtracking/recursion works with strings.

Bonus Tip

• If you want to upskill your coding interview game, you can definitely check out this bestseller course ( this is in Java )