
Problem
- We have infinite number of different type of coins such as coin 1, 2, 3 etc.
- We have been given coins array and amount as input. We need to form combination from coins array that sum up to given amount.

Institution
- Whenever we need to find combination, optimization, min, max , most of the questions are solved by Dynamic Programming.
If you don’t know about Dynamic programming, is not that hard , it’s just people have made it buzz word and tag it as difficult.
- Simply speaking in dynamic programming we try to break down large problems to small problems to get the value for that at first and then move to bigger and bigger subproblems.
- There are two types of approach we follow to solve any dynamic programming problem. Top Down and Bottom Up.
- In this Problem we will come up with both the solution.
Solution
Top Down
- In Top Down approach we break larger problem into small problem. If we have to calculate problem for f(5) , then we first compute f(4). In order to calculate f(4) we first calculate f(3).Likewise we reach to f(0) which becomes our base case.
- It’s more of recursion/backtrack strategy. Best way to understand recursion/backtrack approach is to draw tree diagram to understand all the options for given problem.
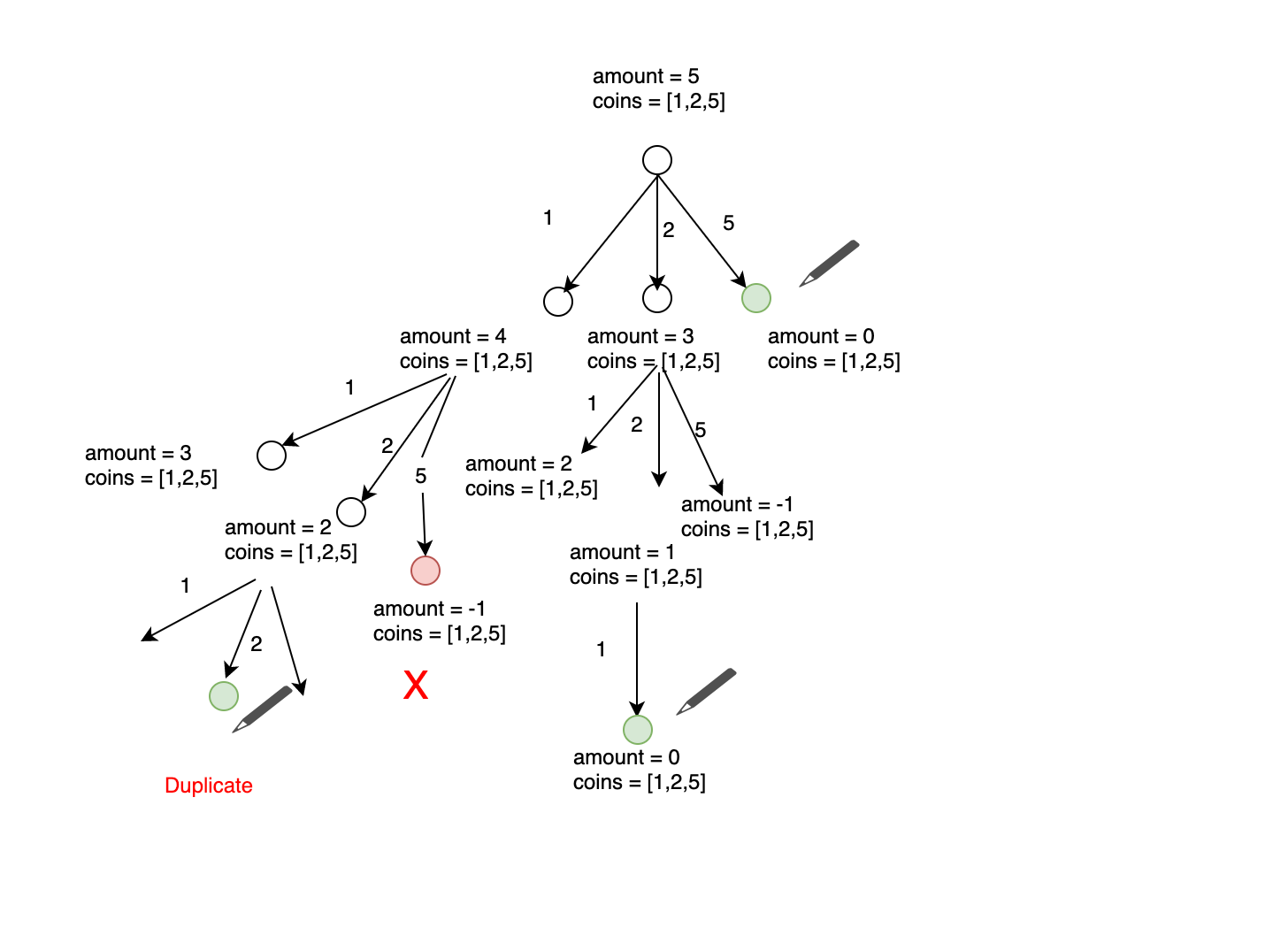
- In above tree diagram, we first see what all are the possibility when the amount to be formed is 5 with coins array. We can use coin 1, 2, 5 and we subtract it from input amount.
- Then for each new amount (Sub Problem) we have again coins 1,2,5 and we subtract them and get new sub problem.
- Likewise for certain case we reaches upto 5 .For some cases we overshoot the value, so basically we cannot form 5 in that case.
- We only select cases where we can form amount 5 and add increase count to return that.
Duplicates Problem
- But there is one problem, since we forming combination, we will end up getting duplicates as well . for example [ 2,2,1] and [1,2,2] are not different combination there are same. but in our logic we are getting duplicates.
- One of the way to avoid duplicates is to use index in incremented ways. What it means that if current index of coin used is 1 then it will only consider coin at index 1 , 2 .. so on and it will not consider index 0.
- In below diagram , when we are using coin 1 , we are considering all the coins . For index 2 we are only considering coin at index 2 and forward. we are not considering coin at index 1 , thats how we can prevent using duplicates.

- In above tree diagram we can observe that there are repeated work that we are doing. For example when amount is 1 and current index is 1 , we are recomputing the answer , so if we use cache to keep the previously calculated answer then we can reuse it . This approach is know as Memoization.
- Below is our code for top down approach.
class Solution {
Map<String, Integer> cache;
public int change(int amount, int[] coins) {
cache = new HashMap<>();
return backtrack(amount, coins, 0);
}
private int backtrack(int amount, int[] coins, int index){
// new combination exist
if(amount == 0){
return 1;
}
// no combination found
if(amount < 0){
return 0;
}
// already computed, return from cache
if(cache.containsKey(index+"#"+amount)){
return cache.get(index+"#"+amount);
}
int res = 0;
// consider only current index and forward
for(int i=index; i<coins.length;i++){
res+=backtrack(amount - coins[i], coins, i);
}
// store the calculated value in cache.
// we are storing index+amount as key in cache
cache.put(index+"#"+amount, res);
return res;
}
}
- We are storing coins index and amount to be calculated as key for cache. If we observer the tree , we will realize index + amount makes each iteration unique .
Submission
- Top down solution is accepted by Leetcode.

Complexity
- Time Complexity : O(N*M)
- Space Complexity: O(N*M)
Where N is length of amount and M is coins size.
Bottom Up
- Bottom up strategy is bit different than top down , but once we come up with top down , bottom is not that different.
- We will create 2D array with coins and amount size, to store the amount at each index.
- Initially we will initialize all counts with 0 when coins are zero because we cannot form amount more than 0.
- We will initialize amount 0 when number of coins are 0 or more to be 1.
- After initialization we are storing count to form amount, considering coins at each index .
- If coins at any index more than amount to be formed than we just copy the count to form previous amount.
- Otherwise we add case when we have one coin less + case when we consider current coin.

public int change(int amount, int[] coins) {
int[][] dp= new int[coins.length+1][amount+1];
// when no coin we cannot form any amount except 0
for(int i=0;i<=amount;i++){
dp[0][i] =0;
}
// we can form amount 0 when we have 0 or more coins
for(int j=0;j<=coins.length;j++){
dp[j][0]=1;
}
for(int i=1;i<dp.length;i++){ // iterating for each # of coins
for(int j=1;j<dp[0].length;j++){ // iterating for each amount
if(coins[i-1]<=j){ // when amount is greater than current coin
dp[i][j]=dp[i-1][j]+dp[i][j-coins[i-1]]; // adding case when we don't consider the current coin + case when we consider current coi
}else{
dp[i][j]=dp[i-1][j]; // when amount is less than coin, then we cannot form any amount hence just copy previous case
}
}
}
return dp[coins.length][amount]; // total count to form amount is stored at last index of coin and amount
}
- Our solution is accepted byLeetcode.

Complexity
- Time Complexity : O(N*M)
- Space Complexity: O(N*M)
Where N is length of amount and M is coins size.
Conclusion
- In this article we solved Leetcode #518 problem. This problem involves knowledge of dynamic programming. We solved it using top down and bottom approach and discussed about the solution detail.
Bonus Tip
- If you want to upskill your coding interview game, you can definitely check out this bestseller course ( this is in Java )
