Blog

How to Solve Number of Provinces ( Leetcode # 547 )

  • Post last modified:December 15, 2022
  • Reading time:6 mins read

Introduction

In this article, we will solve Leetcode problem 547 which help us to learn about graph data structure , recursion and union-find algorithm.

Problem Statement

  • We have given n number of cities. some of them are connected while some are not.
  • If City a connected to b and b connected c then a indirectly connected to c
  • A province is a group of cities that are connected directly or indirectly and doesnt include cities outside of the group
  • We have been given a matrix n*n where each cell value tell us if city i connected to city j.
  • Matrix Index is zero based and nodes are 1 based.
  • We have to return number of provinces in the graph.

Example #1

Input: isConnected = [[1,1,0],[1,1,0],[0,0,1]]
Output: 2
  • For a graph mentioned in the problem statement , we can see node 1 and node 2 are connected to each other hence they make 1 province , while node 3 makes the other province . So, total number of provinces that we can find are 2.

Solution

  • Intuition behind this problem is to traverse the input matrix and for each edge we need to connect the nodes
  • Once we finished traversing we will left with connecting nodes that part of same provinces.
  • But we will not be able to connect single nodes which make themselves a separate province , for example , in below graph node 3 makes itself a another province.
  • If you know union-find algorithm then this problem would be easy to solve but if not let me explain about it first.

Union Find Algorithm

  • In union find algorithm we connect node to each other based on provided edges in adjacency list or in matrix.
  • Lets first define parent and rank hashmap data structure. we will use parent to keep track of parent of the node and rank to track the level of each components.
    HashMap<Integer, Integer> parent = new HashMap<Integer, Integer>();
    HashMap<Integer, Integer> rank = new HashMap<Integer, Integer>();
  • As for initialization we will initialize each with its own value for parent and rank would be initialize as 1.
        for(int i=0;i<isConnected.length;i++){
            parent.put(i, i);
            rank.put(i,1);
        }
  • We will iterate over each edge in the graph and will try to union them. Here value 1 represent there is edge between node i and j. If there is edge exist between the node then union will mark parent as common for the node if node parent will not change.
        int res = 0;
        for(int i=0;i<isConnected.length;i++){
            for(int j=0;j<isConnected[0].length;j++){
                if(isConnected[i][j]==1 && union(i, j)){
                    System.out.println("i,j"+i+","+j);
                    res++;
                    System.out.println("res"+res);
                }
            }
        }

        return isConnected.length-res;

Union

  • We will first find the parent for node 1 and node 2. finding parent is not that difficult since we have initialize parent hashmap with 1. So during intial call parent 1 and parent 2 will be their node itself.
  • Since the both the parents are different we will find the rank , in this case its 1 since we have initialized it so.
  • Rank for both the nodes are same hence we can attach either node1 to node2 and increase node2’s rank or attach node2 to node1 and increase node1 rank.
  • Now when we traverse for the edge (2,1) , in that case now our union method will return same parent and will not require to union it any further since we already did it for edge(1,2)
  • But for edge (3,3) we will not have any nodes to attach hence we will skip that node.
private boolean union(int node1, int node2){
        int parent1 = findParent(node1);
        int parent2 = findParent(node2);
        
        if(parent1==parent2) return false; 
       
        int rank1 = rank.get(parent1);
        int rank2 = rank.get(parent2);
    
        
        if(rank1<rank2){
            parent.put(parent1, parent2);
        }else if(rank2<rank1){
            parent.put(parent2, parent1);
        }else{
            parent.put(parent1, parent2);
            rank.put(parent2, rank.get(parent2)+1);
        }
        
        return true;
}
  • Below is the example of union of node 1 and node 2. as you can see rank of node 2 increases by 1 when we attach node 1 to it along with change of parent for node 1. Now node 1 and node 2 are connected nodes which represent one single province.
  • Since we have now connected all the components we know that how many connected components our graph eventually has by tracking res variable.
  • Since we know the total value of nodes/cities from the problem statement , if we subtract num_of_cities – num_of_components , we will get the num of provinces.
  • In our example number of cities are 3 and number of connected components are 1. so the final result that is number of provinces are 2.

Find

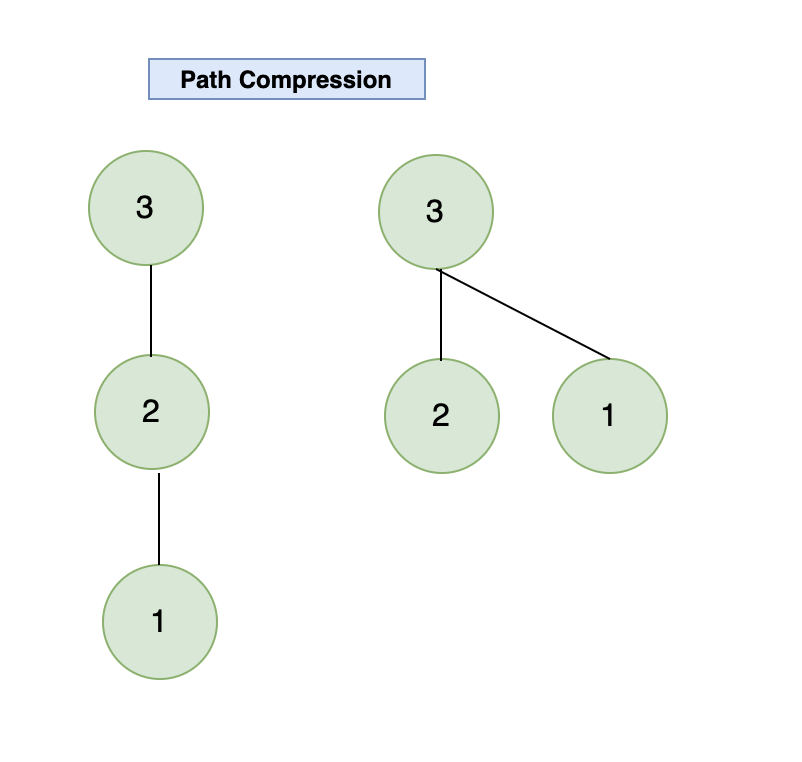
  • Find logic basically finds the parent for the given node. for nested graph parent i.e root node would be at the top hence child has to make recursive call upto root to get the parent. We can actually reduce these calls with logic called path_compression.
  • As you can see we are updating parent for each child node along with recursion call. what it will do for each child node is that , it will mark root node as parent node for each child and for grand child’s as well.
    private int findParent(int node){
        if(node == parent.get(node)){
            return node;
        }
        
        int nodeParent = findParent(parent.get(node));
        parent.put(node, nodeParent);
        return nodeParent;
    }

Final Solution

  • Let’s put together all the logic as a solution for this problem
class Solution {
    HashMap<Integer, Integer> parent = new HashMap<Integer, Integer>();
    HashMap<Integer, Integer> rank = new HashMap<Integer, Integer>();
    
    public int findCircleNum(int[][] isConnected) {
        
        for(int i=0;i<isConnected.length;i++){
            parent.put(i, i);
            rank.put(i,1);
        }
        
        int res = 0;
        for(int i=0;i<isConnected.length;i++){
            for(int j=0;j<isConnected[0].length;j++){
                if(isConnected[i][j]==1 && union(i, j)){
                    System.out.println("i,j"+i+","+j);
                    res++;
                    System.out.println("res"+res);
                }
            }
        }
        
        return isConnected.length-res;
    }
    
    
    private int findParent(int node){
        if(node == parent.get(node)){
            return node;
        }
        
        int nodeParent = findParent(parent.get(node));
        parent.put(node, nodeParent);
        return nodeParent;
    }
    
    
    private boolean union(int node1, int node2){
        int parent1 = findParent(node1);
        int parent2 = findParent(node2);
        
        if(parent1==parent2) return false; 
       
        int rank1 = rank.get(parent1);
        int rank2 = rank.get(parent2);
    
        
        if(rank1<rank2){
            parent.put(parent1, parent2);
        }else if(rank2<rank1){
            parent.put(parent2, parent1);
        }else{
            parent.put(parent1, parent2);
            rank.put(parent2, rank.get(parent2)+1);
        }
        
        return true;
    }
}

Result

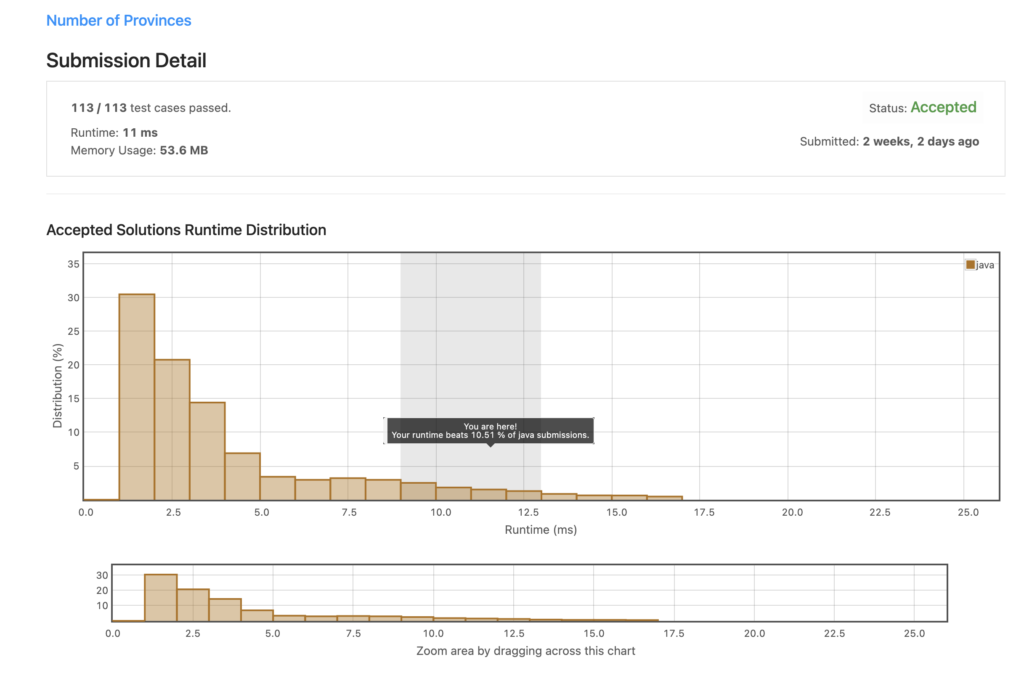
  • Our results passed 113 test cases and get accepted by leetcode. although performance is 10% i am not sure if there is further optimization available for this problem
  • Anyway , TC for this problem is O(N^2*logN) where N is number of nodes.
    SC will be O(N) for using 2 Hashmap’s.

Conclusion

  • In this blog we solved leetcode 547 problem that require the knowledge of graph data structure and union-find algorithm.

Bonus Tip

  • If you want to upskill your coding interview game, you can definitely check out this bestseller course ( this is in Java )

Tags: , , , ,

Leave a Reply