Blog

Maximum Nesting Depth of the Parentheses — Leetcode 1614 ( Ruby Solution )

  • Post last modified:January 12, 2023
  • Reading time:3 mins read

Introduction

  • In this article, we will solve Leetcode 1614, which will mainly help us understand how we can use a stack data structure.
  • We will also see how we can solve it without a stack data structure

Problem Statement

  • We have been given a Valid Parentheses String(VPS) and need to return nesting depth.
  • VPS is defined as 
    >> “” -> empty string 
    >> it is written as AB, where A and B both are valid VPS
    >> (A) -> where A is VPS

Examples

  • In the below example, the depth of parentheses is 3 since the digit 8 is nested inside of 3 parentheses.
  • Similarly in the second example, nested depth is 3, where 3 is nested parentheses.

Solutions

Intuition

  • Intuition is that we iterate through each character of the string and if the character happens to be open parentheses then we add it to our stack.
  • When we add open parentheses to the stack, we also check if the current stack size is greater than the max or not. Stack size basically depicts the depth.
  • If the character happens to be closing parentheses then we can pop the last open parentheses that we added since it completes our parentheses.

Code

  • Below is the code where we are using array as a stack.
# @param {String} s
# @return {Integer}
def max_depth(s)
    stack = []
    max = 0;
    s.split('').each do |c|
        if c == '('
            stack.push(c)
            max = max > stack.size ? max : stack.size
        elsif c == ')'
            stack.pop()
        end
    end
    max
end
  • We can avoid using stack since the only character we are dealing with is open and closing parentheses.
  • Instead, we can maintain open parentheses and increment whenever open parentheses encounter and decrease when closing parentheses are encountered.
def max_depth(s)
    max = 0;
    depth = 0;
    s.split('').each do |c|
        if c == '('
            depth+=1
            max = max > depth ? max : depth
        elsif c == ')'
            depth-=1
        end
    end
    max
end

Result

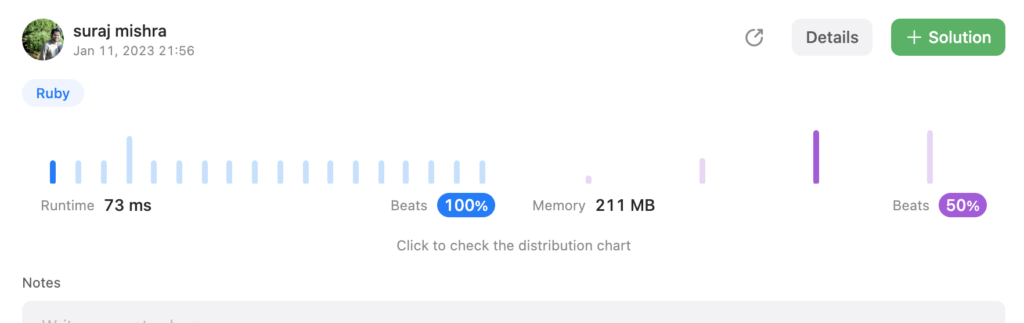
  • Our solution is accepted by leetcode.

Complexity

With Stack
-> Time Complexity: O(N)
-> Space Complexity: O(N)

Without Stack
-> Time Complexity: O(N)
-> Space Complexity: O(1)

Conclusion

  • In this article, we used the stack to solve the parentheses problem. This problem is good to start problem to play with the stack data structure.
  • We also see how we can make the stack redundant if the data that is stored in the stack are not changing.

Bonus

  • If you want to upskill your coding interview game, you can definitely check out this bestseller course ( this is in Java )
Tags: , , , ,

Leave a Reply